An Easy and Brief Introduction to Bose Gas and Fermi Gas

This post is meant to highlight the physical interpretation and results for Bose Gas and Fermi Gas. The level of math is tame to suit audiences with less mathematical exposure.

Problem for Ideal Gas

By equipartition theorem, \(E=\frac{3}{2}kT\) for \(1\) mole of ideal gas. This corresponds to \(\frac{3}{2}k\) for \(C_V\), the heat capacity. This indicates that heat capacity of an ideal gas is constant and non-zero for all temperatures.

This violates Third Law of Thermodynamics, which states that \(\lim_{T \to 0} C_V = 0\)

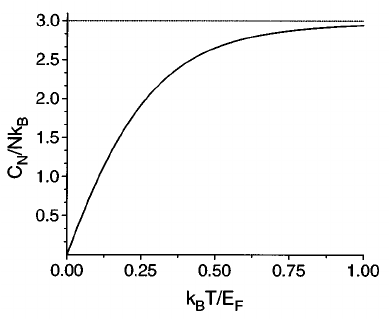
Fermi Gas

There are two types of particles. Some have spin in integer values (called bosons) and some have spin in odd half integer values (called fermions).

The main difference lies in the fact that fermions have to obey Pauli Exclusion Principle, which states that two fermions have to occupy different quantum states. This makes the energy of fermions higher for lower temperature, as fermions are forced to occupy states with higher energy. This effect minimises as \(T\) increases and the energy approaches that of classical gas. (Correspondence Principle!)

It can be be verified that heat capacity at low temperatures appraoch \(0\).

(Source of Image)

Bose Gas

At low temperatures, Bose-Einstein Condensate appears, which means most of the particles are dragged to the ground state with lower energies. This causes the energy to be significantly lower than classical gas (at least for very low temperatures). It eventually approach the classical limit. (Again correspondence Principle!)

It can be be verified that heat capacity at low temperatures appraoch \(0\).

(Source of Image)

A Plot of Energy of Different Gases

(Source of Image)

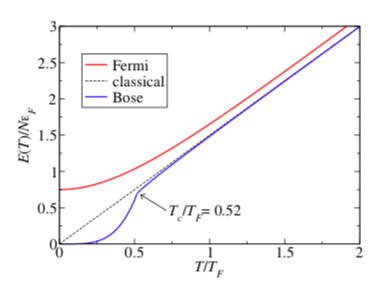
This illustrates how quantum effects can be used to explain the inaccuracies in classical physics.