Julia Sets and the Mandelbrot Set

Here we explore the relationships between Filled-in Julia Sets and the Mandelbrot Set.

In this article we consider the function: \(f_c: z \mapsto z^2+c\), where \(c\) is a constant.

We then define \(K_c\), which is also known as the Filled-in Julia Set, as the set of \(z\) which are non-escaping under continuous iterations of \(f_c\). In other words:

\[K_c=\left\{z \in \mathbb{C} \mid\left(f_c^n(z)\right)_{n \in \mathbb{N}}, \text { is bounded}\right\}.\]

Where \(f_c^n(z)\) denotes the \(n^{\text {th}}\) iteration of the function \(f_c\) on \(z\).

Furthermore, define \(n_{\text{max}, R}(z)\) as the largest \(k\) such that the magnitude of \(f_c^k(z)\) is smaller than \(R\) (In the graphs below, we take \(R=1000\)).

We are concerned with whether \(K_c(z=0)\) is bounded, which means whether \(n_{\text{max}, R}=\infty\). (In other words, whether the point \(z=0\) escapes to infinity under continuous iterations of the function \(f_c: z \mapsto z^2+c\).)

On an Argand Diagram, we are plotting the Real Axis of \(c\) vs the Imaginary Axis. If \(K_c(z=0)\) is bounded, mark the corresponding point of \(c\) as a darker colour for a higher \(n_\text{max}\), and lighter colour for a small \(n_\text{max}\).

We thus obtain the Mandelbrot Set:

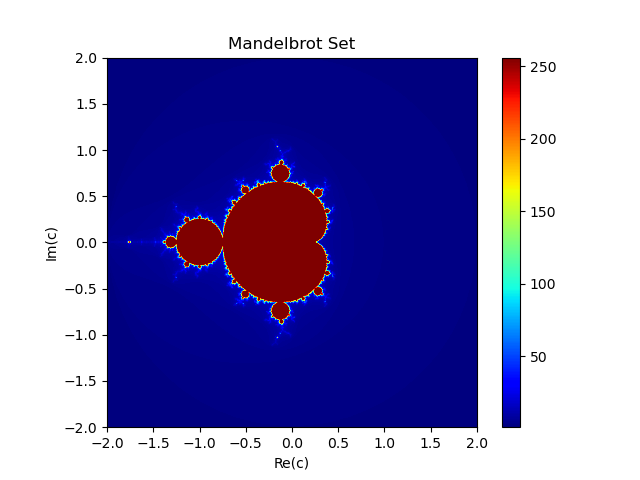
Notice that the boundary of the Mandelbrot Set has no “punctures” or “holes”. In other words, it is compact. (Thus closed and bounded by Heine-Borel Theorem).

Enlarging the image of the Mandelbrot Set will result in a connected image (with finer and finer details!). This is related to the MLC Conjecture, which states that the Mandelbrot set is locally connected.

Connectiveness of Filled-in Julia Sets

We can colour Julia Sets using a similar method as above: For a fixed \(c\), find the \(n_\text{max}\) for each \(z\). For a higher \(n_\text{max}\), denote it with, say, a lighter colour (as long as the colour is contrast is large enough)

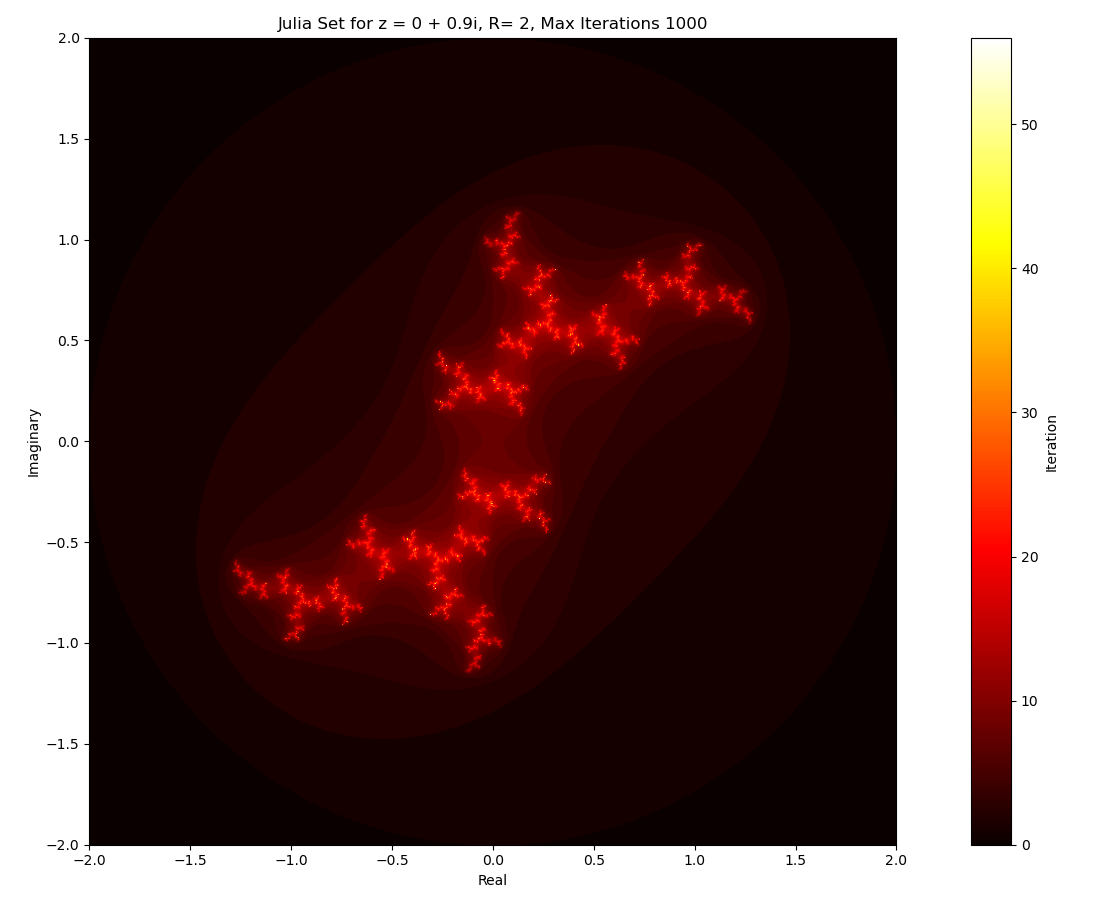
Dichotomy theorem

If \(c\) is in the Mandelbrot set, the corresponding Julia Set is connected. Otherwise, it is disconnected. Observe the image above. As it is not connected, the corresponding \(c\) (which is \(0.9i\)) is not in the Mandelbrot Set! (we can observe this in Figure 1).

Conclusion

Filled-in Julia Sets: Given \(c\) (defined each time), find behaviour of \(z\) (upon continuous iterations of \(f_c\)).

Mandelbrot Sets: Given \(z\) (Must be \(z=0\)), find behaviour of \(c\). (Whether the value of \(c\) will make \(z=0\) escape or not).

The two sets are connected by the Dichotomy Theorem, so by looking at the Mandelbrot set we can know which Julia Sets are connected and which are disconnected (for example if magnitude of \(c\) is larger than \(2\), the corresponding filled-in Julia Set must be disconnected).

Exercises for the Readers

• Write a python code that plots the Mandelbrot set, and the Julia set. (Difficulty: University Year 1)
• Defining \(T=\left\{\left(x, \sin \frac{1}{x}\right): x \in(0,1]\right\} \cup\{(0,0)\}\), show that it is connected but not locally connected. Show the relation of \(T\) to the Mandelbrot set. (Difficultly: University Year 2-3)

Last Updated - 3/6/2024