Symplectic Integrators

This is the second post on my summer research about three-body problems. Today we are discussing Symplectic Integrators.

This is my previous post about the figure-8 orbit if you have missed it.

Definition of Symplectic Integrators

First we need to look at Liouville’s Theorem in Hamiltonian Dynamics. We consider a energy-conserved system. As seen in the figure below upon a transformation of coordinates, \(dA=dA'\).

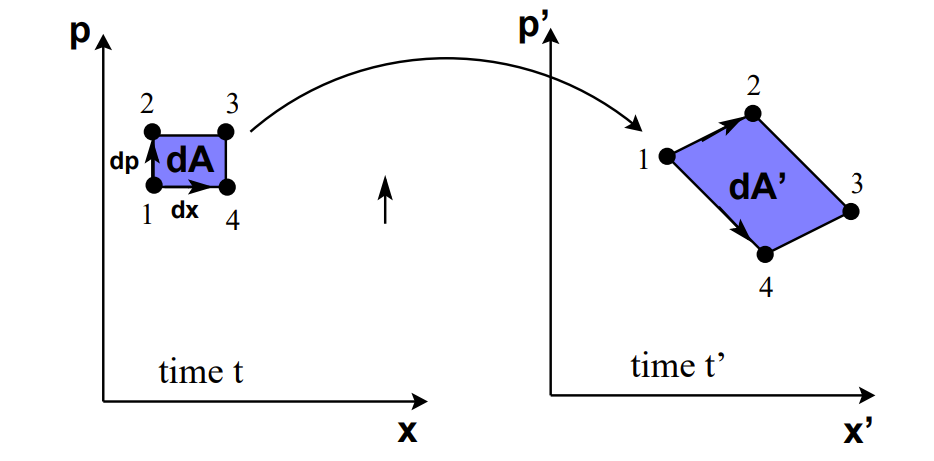
Thus, the result of integration of Newton’s laws by a finite amount of time can be represented as an area preserving map.

This is very important as this leads to energy conservation! The reader can verify that Euler’s Method and RK4 are not sympletic integrators and will not conserve energy.

How to Identify Symplectic Integrators

Consider:

\[\binom{x_{n+1}}{p_{n+1}}=A\binom{x_n}{p_n}\]

If determinant of \(A\) is \(1\), it is symplectic.

Implementation in my code

Consider:

\[\begin{aligned} & x_{i+1}=x_i+c_i v_{i+1} t \\ & v_{i+1}=v_i+d_i a\left(x_i\right) t \end{aligned}\]

Now for 3rd-order Symplectic Integrators, we can have:

\[c_3 = \left[1, -\frac{2}{3}, \frac{2}{3}\right]\] \[d_3 = \left[-\frac{1}{24}, \frac{3}{4}, \frac{7}{24}\right]\]

For 4th-order Symplectic Integrators, we can have:

\[c_4 = \left[\frac{1}{2(2 - 2^{1/3})}, \frac{1 - 2^{1/3}}{2(2 - 2^{1/3})}, \frac{1 - 2^{1/3}}{2(2 - 2^{1/3})}, \frac{1}{2(2 - 2^{1/3})}\right]\] \[d_4 = \left[\frac{1}{2 - 2^{1/3}}, -\frac{2^{1/3}}{2 - 2^{1/3}}, \frac{1}{2 - 2^{1/3}}, 0\right]\]

The readers can check it is sympletic.

Accuracy of higher order similations

For the Figure-8 orbit, I run it \(50000\) times, with a \(0.01\) timestep.

For a 4th-order Symplectic Integrator, the energy deviation is \(1.9451494605089267 \times 10^{-08}\).

For a 3rd-order Symplectic Integrator, the energy deviation is \(4.1499441141427045 \times 10^{-08}\).

For a 2nd-order Symplectic Integrator (Verlet Method we have used all along), the energy deviation is \(5.9073950710067754 \times 10^{-05}\).

Therefore we can conclude we have improved the accuracy of our simulation!

Problems and limitations

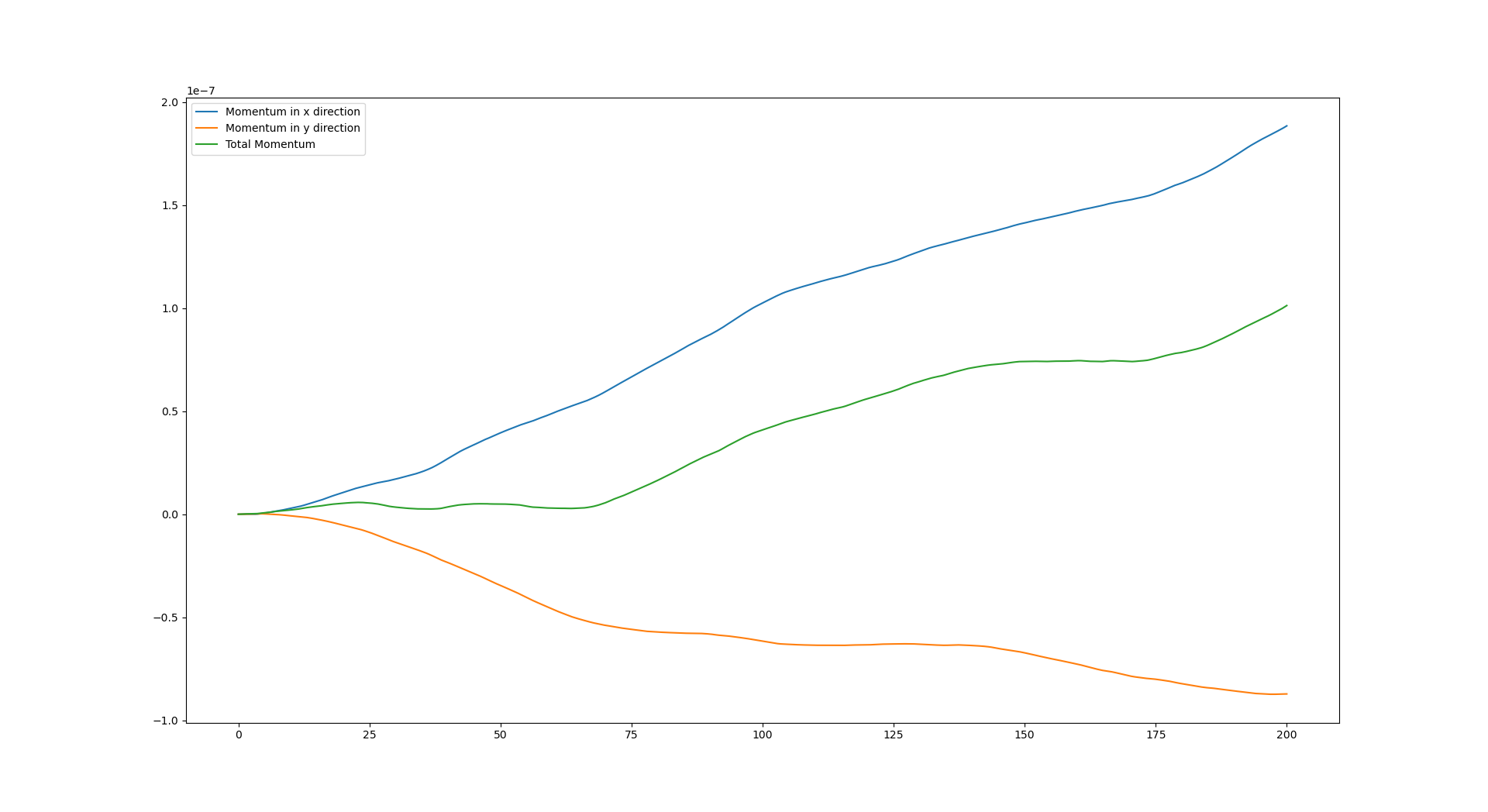
Momentum is not conserved as our system. Even though the error is very small, it increases with time, which is slightly concerning.

Having Fun

I think it is still more important to enjoy my days doing the summer project, as it’s a time when I do not need to worry too much about my grades. I definitely enjoy doing this project, as the animations are truely beautiful!

Here is an animation of a “knocked-off Figure-8”:

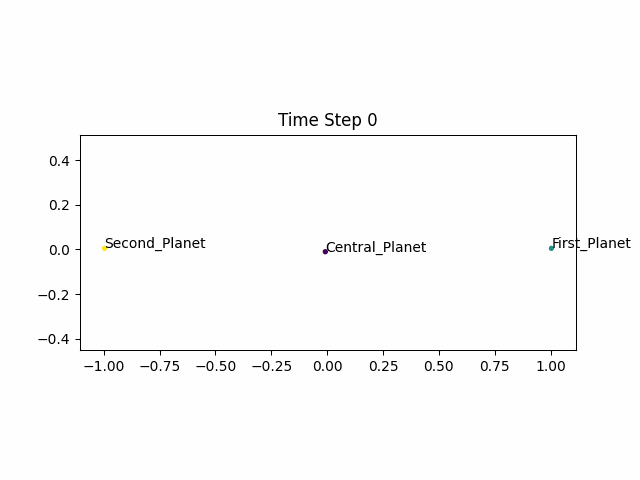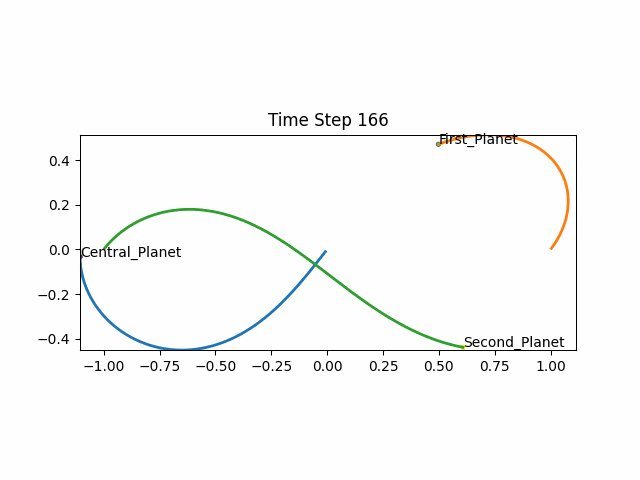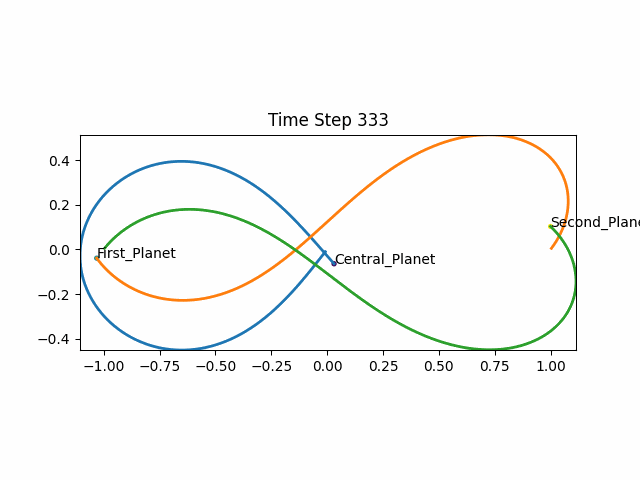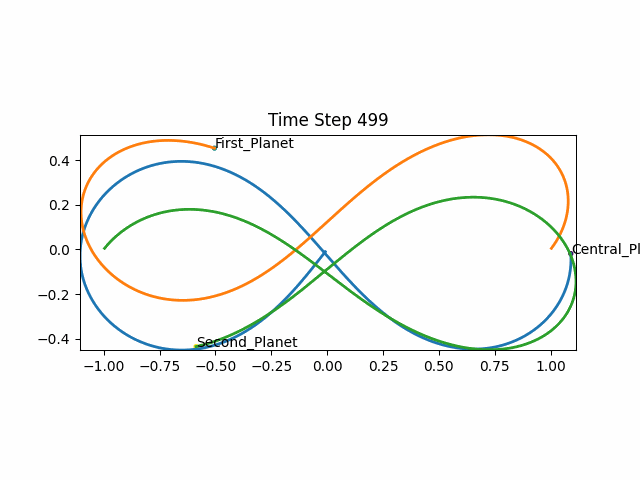
Credits

For the first part, “Definition of Symplectic Integrators”, the image and the content are heavily inspired by this PDF written by Peter Young.

I would also like to thank Dr Jenni Smillie for her guidance and support duing this project.