Theorema Egregium — The reason why all maps are wrong
Theorema Egregium states that isometric surfaces have the same gauss(ian) curvature. Equivalently, surfaces with different gauss curvature are not isometric (with same First Fundamental Forms).
Gauss Curvature of a Sphere
First note that the Gauss Curvature on the whole sphere is uniform. Next notice that the surface area of a sphere is \(4 \pi R^2\). By Gauss-Bonnet Theorem:
\[\begin{align} \chi(\Sigma) &= \frac{1}{2\pi}\int_{\Sigma} K \\ &=\frac{1}{2 \pi } (4 \pi R^2)(K) \\ &=(2R^2)(K) \end{align}\]Where \(\chi(\Sigma)\) is the Euler Characteristic. As the sphere has no holes or punctures, the Euler Characteristic is 2. (Briefly introducted in Primary School!)
Hence, \(K=\frac{1}{R^2}\).
Gauss Curvature of a Plane
By definition (or intuition), a plane has \(0\) Gauss Curvature. This shows that a sphere and a plane have different Gauss curvatures!
Isometric Surfaces
Isometric Surfaces have the same measurement of distances and angles and are related by “bending” (As seen below).

(Isometric deformation from a catenoid to a helicoid. Source: Wikipedia)
Conclusion
This is the reason behind all world maps are wrong - a plane and a sphere have different Gaussian curvatures, therefore it is impossible for a map to both describe the angles and distances of the earth accurately.
The common world map does not preserve Area. This is a reason the size of india is often underestimated. (It is much bigger than you would think!)
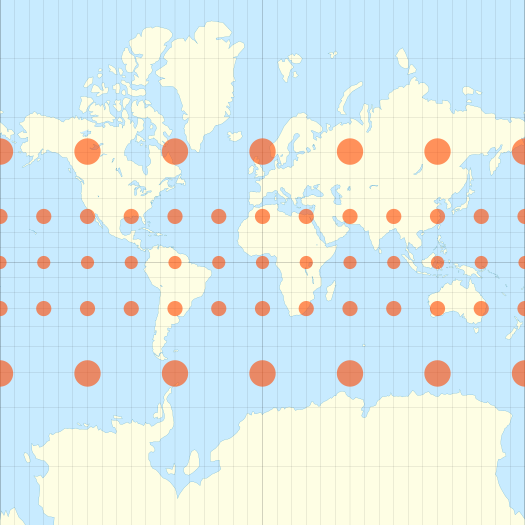
(Image from Wikipedia)
There are other types of maps that only preserve geodesics (shortest distances). However, these aren’t particular aesthetic, and therefore not commonly used.
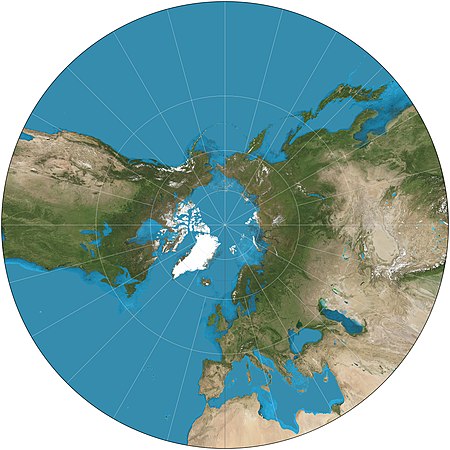
(Image from Wikipedia)
Exercises for the Reader
- In the first sentence, we stated that Theorema Egregium implies isometric surfaces have the same gauss curvature. Why is it equivalent to surfaces with different gauss curvature are not isometric? (Difficulty: University Year 1)
- Show that helicoids and catenoids are isometric surfaces. (Difficulty: University Year 2-3)
- If I deform the sphere, how will the gauss curvature change? Why? (Difficulty: University Year 2-3)
- (***) Irrelevant: Show the physical intepretation of the first fundamental form and the second fundamental form. Show that the third fundamental form (defined by \(\mathrm{d}N \cdot \mathrm{d}N\)) is redundant (Too hard? Answers in my other post).
