Infinite Descent and Vieta’s Formulas

Let \(a\) and \(b\) be positive integers such that \(ab + 1\) divides \(a^2 + b^2\). Show that \(\frac{a^2 + b^2}{ab + 1}\) is the square of an integer.

Assumptions

Assume there exist positive integers \((a, b)\) for which \(k = \frac{a^2 + b^2}{ab + 1}\), and \(k\) is not a perfect square.

Let \((A, B)\) be positive integers that satisfy the above question such that \(A+B\) is minimal. WLOG assume \(A \geq B\).

Quadratic Formula

Therefore, we arrive at:

\[\begin{equation} A^2+B^2=k(AB+1) \\ \implies A^2-(kB)A+(B^2-k)=0 \end{equation}\]

We can see that \(A\) is the root to \(x^2-(kB)x+(B^2-k)=0\). We know there are two roots for a quadratic formula, so let \(C\) be the other root.

Vieta’s Formula

By Vieta’s Formula (Sum of Roots and Product of Roots as introduced in High School):

We have

\[A+C=kB\]

and

\[(A)(C)=B^2-k\]

The latter implies:

\[C=\frac{B^2-k}{A}\]

Showing Contradiction

As we assumed \(A \geq B\), we have:

\[\begin{align} B^2-k &\leq A^2-k< A^2 \\ \implies \frac{B^2-k}{A} &< A \\ \end{align}\]

The left hand side is \(C\) as found above, so we have \(C<A\).

Therefore we have \(C\) that satisfies all the conditions, but \(C+B<A+B\), which is a contradiction to the minimality requirement above.

Therefore \(\frac{a^2 + b^2}{ab + 1}\) must be a perfect square.

Visualization

Above shows that there is no minimal solution that satisfy the equation above. It can be visualized through Python that if \(k\) is a perfect square, there exists a minimal solution. This process of “jumping” of solutions is called the Vieta Jumping.

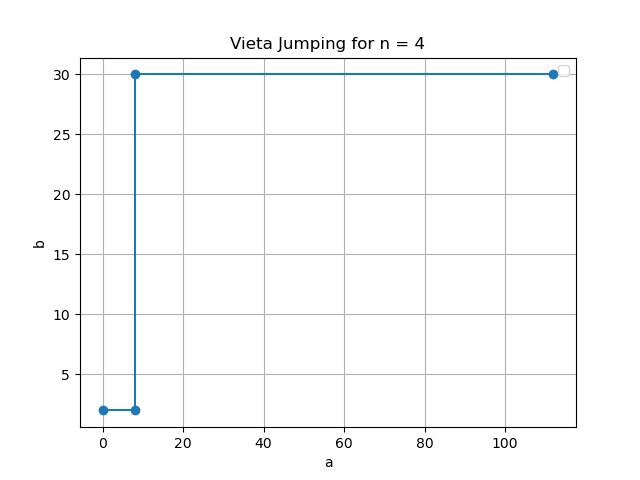
Corresponding to:

\[\begin{align*} 1: & \quad a = 0, b = 2 \\ 2: & \quad a = 2, b = 8 \\ 3: & \quad a = 8, b = 30 \\ 4: & \quad a = 30, b = 112 \\ \end{align*}\]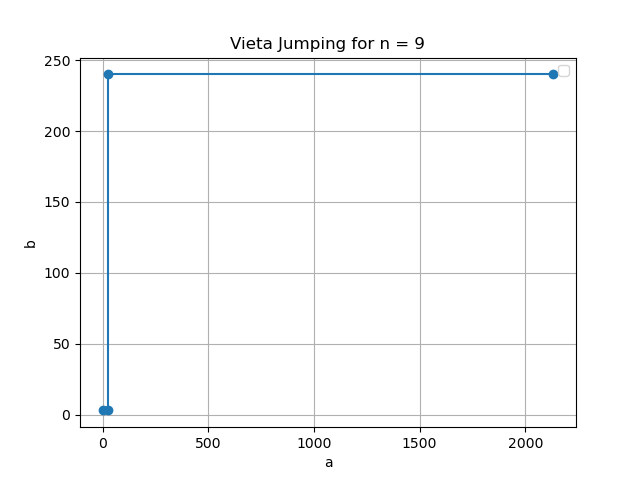

Corresponding to:

\[\begin{align*} 1: & \quad a = 0, b = 3 \\ 2: & \quad a = 3, b = 27 \\ 3: & \quad a = 27, b = 240 \\ 4: & \quad a = 240, b = 2133 \\ \end{align*}\]

Code

import matplotlib.pyplot as plt

def find_initial_points(n, max_range=4000):
    points = []
    for a in range(0, max_range):
        for b in range(a + 1, max_range):
            if (a**2 + b**2) % (a * b + 1) == 0:
                if (a**2 + b**2) // (a * b + 1) == n:
                    points.append((a, b))
    return points

def plot_initial_points(points, n):
    fig, ax = plt.subplots()
    x_coords = [x for x, y in points]
    y_coords = [y for x, y in points]

    ax.plot(x_coords, y_coords, marker='o', linestyle='-')

    ax.set_xlabel('a')
    ax.set_ylabel('b')
    ax.set_title(f'Vieta Jumping for n = {n}')
    plt.grid()
    plt.legend()
    plt.show()

n = 9
number_of_points_plotted = 4  

initial_points = find_initial_points(n)

if initial_points:
    print(f'Found initial points for n = {n}:')
    for idx, (a, b) in enumerate(initial_points):
        print(f'{idx + 1}: a = {a}, b = {b}')

    # Flip the order of points every turn
    for i in range(len(initial_points)):
        if i % 2 == 1:
            initial_points[i] = initial_points[i][::-1]

    # Plot the found initial points
    plot_initial_points(initial_points[:number_of_points_plotted], n)
else:
    print('No initial points found')

Exercises for the reader

• I have intentionally not checked one of the conditions imposed on \(C\). What is it? Formulate a proof to show that it is valid.
• State and prove the general case for Vieta’s Formula and show that in the special case, it becomes the formula we showed above.
• Let \(a\) and \(b\) be positive integers. Show that if \(4ab - 1\) divides \((4a^2 - 1)^2\), then \(a = b\). (2007 IMO Q5)

Credits

This question is the infamous IMO 1988 Q6. The solution is based on this website and this video.