Sundman’s Power Series Solution to the Three Body Problem (Part II)

This is the eighth post on my summer research about three-body problems. Today we are continuing our discussion on Sundman’s Power Series, showing why the series is impractical to be used. I have a brief introduction on this particular problem in the previous post.

Lagrange’s Solution to the Three Body Problem

In 1772, Lagrange found a family of solutions in which the three masses form an equilateral triangle at each instant. These correspond to either L4 or L5 lagrange points, also known as trojan points.

If the mass ratio between the two large masses is below \(24.96\), the orbit will be unstable and any small perturbations will cause their tracks to deviate. This is shown below:

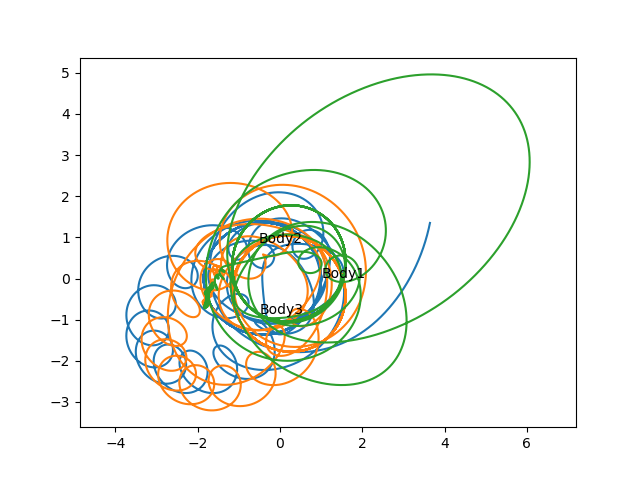
As seen in the trajectories, in a perfect scenario, the trajectories should form a circle. This can be parametrized as:

\[(x,y) = (\cos(t), \sin(t)).\]

From the previous post, we can easily see that:

\[\Gamma = (1-e^{\frac{1}{l}})^3\]

As \(t=\Gamma w\), we can see:

\[t=\frac{2 \Omega \Gamma}{\pi} \log {\frac{1+\tau}{1-\tau}}\]

This can be approximated as:

\[t=\frac{4 \Omega \Gamma}{\pi} (\tau + \frac{\tau^3}{3} + \frac{\tau^5}{5}+ O(\tau^6))\]

We can thus express \(\cos(t)\) and \(\sin(t)\) as:

\[\begin{aligned} \cos(t) &= 1 - 2A^2 \tau^2 - (\frac{4}{3} A^2 - \frac{2}{3} A^4) \tau^4 - (\frac{45}{46}A^2 - \frac{8}{9} A^4 + \frac{4}{45} A^6) \tau^6+O(\tau^8) \\ \sin(t) &= 2A \tau + (\frac{2A}{3} - \frac{4}{3} A^3) \tau^3 + (\frac{2A}{5} - \frac{4}{3}A^3 + \frac{4}{15} A^5) \tau^5 + O(\tau^7) \end{aligned}\]

Now consider the case where \(m_1 = m_0\) and \(m_2 = 1 - 2m_0\).

So, \((m_0, m_1, m_2) = (m_0, m_0, 1-2m_0)\).

Take \(m_1 = \frac{1}{200}\). This corresponds to \(\Omega < 9 \times 10^{-8}\), which corresponds to \(A < 4 \times 10^{-8}\).

Now consider \(t=1\). This corresponds to:

\[t=\frac{4 \Omega \Gamma}{\pi} (\tau + \frac{\tau^3}{3} + \frac{\tau^5}{5}+ O(\tau^6)).\]

For a one decimal accuracy, we want:

\[\sum_ {k=1}^{n} (\frac{4 \Omega \Gamma}{\pi})(\frac{\tau^{2k-1}}{2k-1})>0.9\]

Letting \(\frac{4 \Omega \Gamma}{\pi}\) as \(A\), we have:

\[S_\tau = \sum_{k=1}^{n} {\frac{\tau^{2k-1}}{2k-1}} > \frac{9}{20A}\]

The reader can show that \(A< 4 \times 10^{-8}\) corresponds to \(S_{\tau} > 10^7\).

Now relate this with the series:

\[S=\sum_{k=1}^{p} \frac{1}{2p-1}\]

It has been shown that \(p>e^{2S-2.4}\), and therefore \(p>e^{2S_{\tau}-2.4}\). This corresponds to \(p>10^{8 \times 10^{6}}\).

As \(n>p\) (our series add up slower than the geometric series with odd terms, as \(\vert \tau \vert < 1\)), we can see that \(n>10^{8 \times 10^{6}}\). This shows the sundman series converges too slow and is very impractical to use.

Progress

The coding parts of the project is mainly done. I can finally focus more on the theory behind, which means I have to write more posts, which will greatly help my final report.

It has been 3/4 weeks since I started the project, and in general things work quite smoothly and much better than I originally expected.

Credits

This post is based on the paper by Donald K.Yeomans and Belorizky’s Paper.

I would like to thank Dr Jenni Smillie for her guidance and support duing this project.