Problem of Two Fixed Centers (Part I)

This is the fourth post on my summer research about three-body problems. Today we are discussing the problem of two fixed centers, or more famously, Euler’s three-body problem.

This is my previous post about the two body problem if you have missed it.

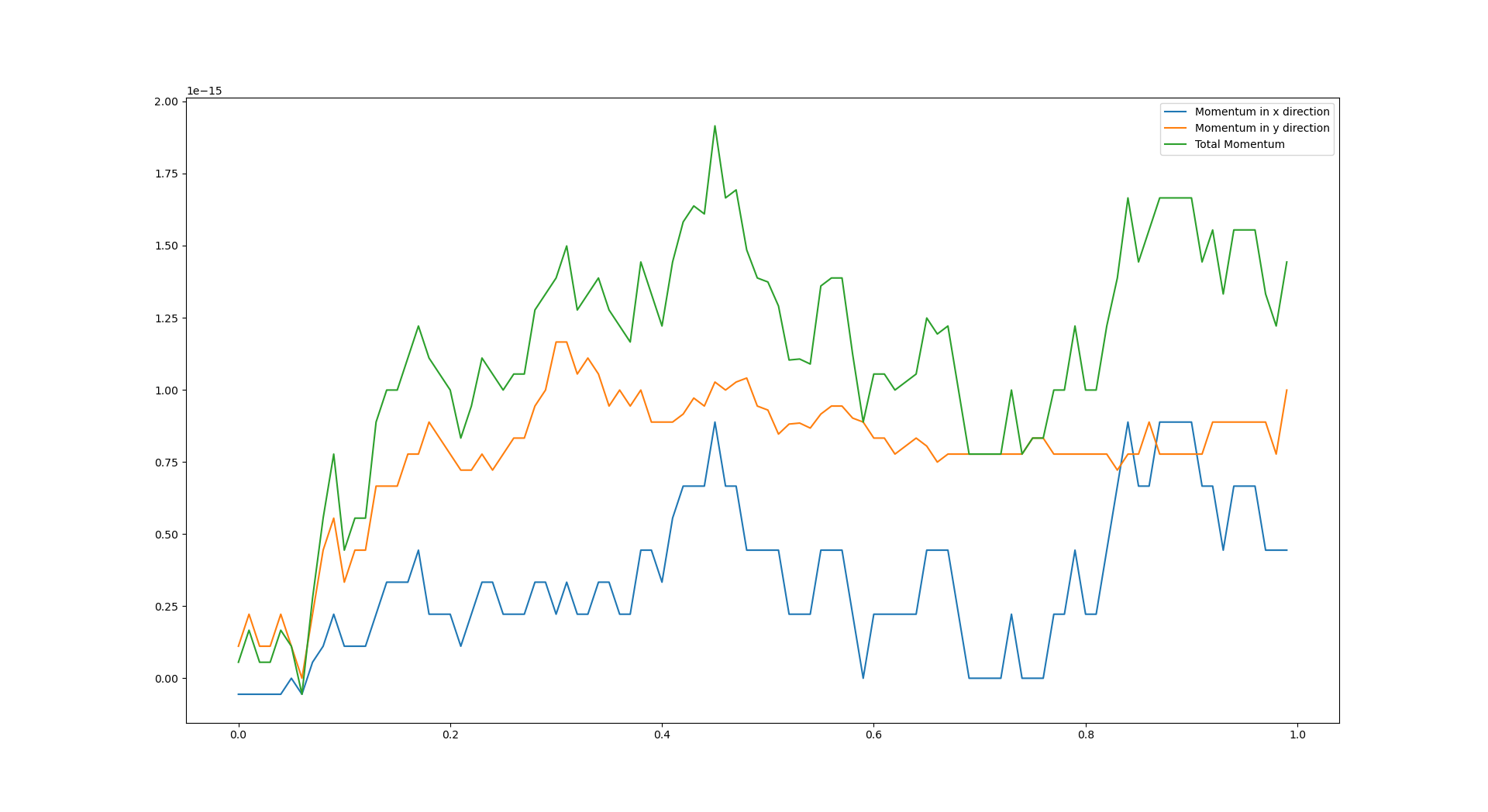
Momentum Unconserved Problem Solved!

A few days ago I mentioned that momentum is not conserved in my system. This is due to a very stupid mistake I later realized… I forgot to set the sum of momentum of each components to \(0\) after each loop! Now it looks much more reasonable.

Problem Set-Up

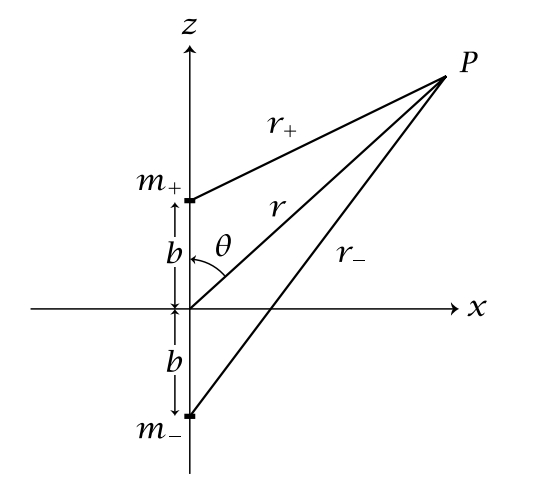
(Source: Integrable Systems in Celestial Mechanics)

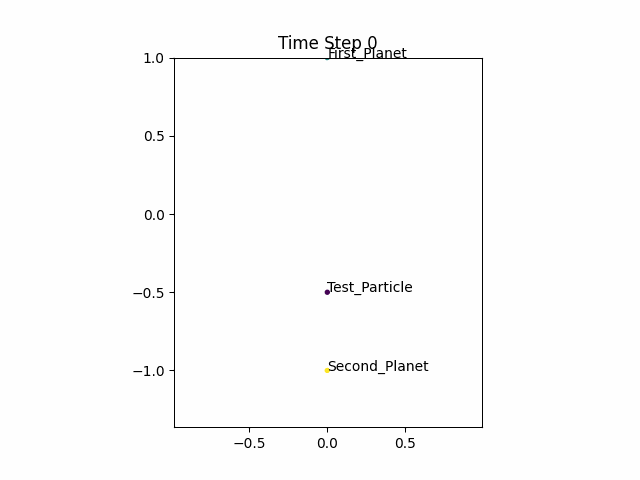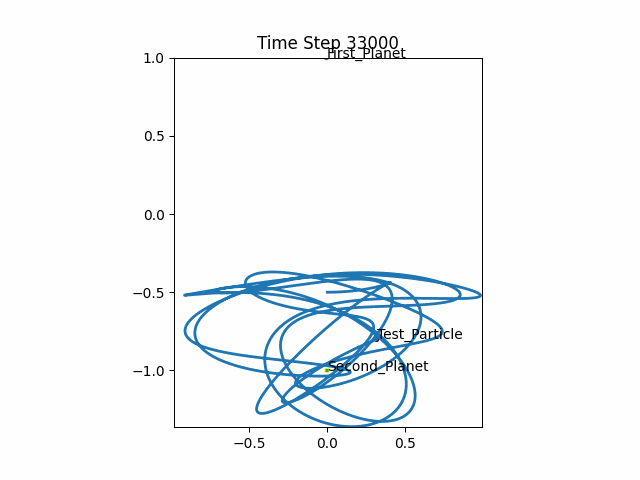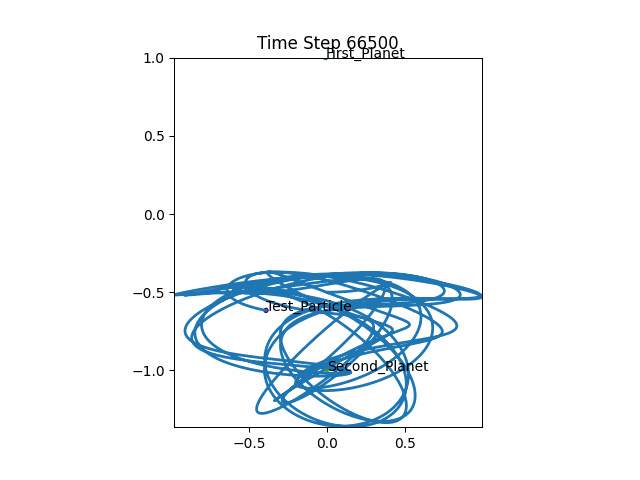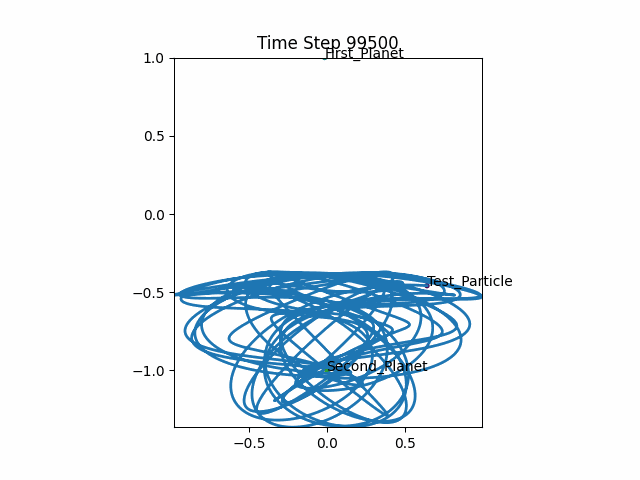
Python implementation

I set two of the masses as “stationary” and messed around with the code for a few hours.

Lagrangian of the System

Rewriting in spheroidal coordinates, we have:

\[r \sin \theta=x= \pm \sqrt{R^2-b^2} \sin \sigma\]

and

\[r \cos \theta=z=R \cos \sigma\]

As we have:

\[\mathbf{r}(R, \sigma) = \begin{pmatrix} x(R, \sigma) \\ z(R, \sigma) \end{pmatrix}\]

We can deduce:

\[\frac{\partial x}{\partial R} = \pm \frac{R \sin \sigma}{\sqrt{R^2 - b^2}}, \quad \frac{\partial z}{\partial R} = \cos \sigma\] \[\frac{\partial x}{\partial \sigma} = \pm \sqrt{R^2 - b^2} \cos \sigma, \quad \frac{\partial z}{\partial \sigma} = -R \sin \sigma\]

We can thus calculate the partial derivatives:

\[\mathbf{r}_R = \frac{\partial \mathbf{r}}{\partial R} = \begin{pmatrix} \frac{R \sin \sigma}{\sqrt{R^2 - b^2}} \\ \cos \sigma \end{pmatrix}\] \[\mathbf{r}_\sigma = \frac{\partial \mathbf{r}}{\partial \sigma} = \begin{pmatrix} \sqrt{R^2 - b^2} \cos \sigma \\ -R \sin \sigma \end{pmatrix}\]

and calculate the metric components using:

\[g_{RR}= \mathbf{r_R} \cdot \mathbf{r_R}\]

and so on.

The reader should be able to obtain:

\[g_{RR}=\frac{R^2-b^2 \cos ^2 \sigma}{R^2-b^2}, \quad g_{R \sigma}=0, \quad g_{\sigma \sigma}=R^2-b^2 \cos ^2 \sigma .\]

Without proof, I will state that:

\[V=-\mu \frac{R+\beta b \cos \sigma}{R^2-b^2 \cos ^2 \sigma}\]

Where:

\[\beta=\frac{m_{+}-m_{-}}{m_{+}+m_{-}}\]

Thus,

\[\begin{aligned} L & =T-V \\ & =\frac{1}{2} \frac{R^2-b^2 \cos ^2 \sigma}{R^2-b^2} \dot{R}^2+\frac{1}{2}\left(R^2-b^2 \cos ^2 \sigma\right) \dot{\sigma}^2+\mu \frac{R+\beta b \cos \sigma}{R^2-b^2 \cos ^2 \sigma} \end{aligned}\]

Jacobian Elliptic Functions

It is hard to explain how it leads to here (just read the book), but at some point I need to solve the equation:

\[S^{\prime 2}=\left(1-S^2\right)\left[1-k_{01}^2 S^2\right]\]

It has solution:

\[S=\operatorname{sn}\left[f+\omega: k_{01}\right]\]

Where \(\operatorname{sn}\) as an example of Jacobi elliptic functions. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. Now we need to know:

\[\frac{d}{du} \operatorname{sn}(u \mid k) = \operatorname{cn}(u \mid k) \operatorname{dn}(u \mid k)\]

Given that \(S = \operatorname{sn}(f + \omega \mid k_{01})\), we can write:

\[S' = \frac{d}{df} \operatorname{sn}(f + \omega \mid k_{01}) = \operatorname{cn}(f + \omega \mid k_{01}) \operatorname{dn}(f + \omega \mid k_{01})\]

Now, let’s square \(S'\):

\[S'^2 = \left( \operatorname{cn}(f + \omega \mid k_{01}) \operatorname{dn}(f + \omega \mid k_{01}) \right)^2\]

From the properties of Jacobi elliptic functions, we have the following identities:

\[\operatorname{sn}^2(u \mid k) + \operatorname{cn}^2(u \mid k) = 1\] \[\operatorname{dn}^2(u \mid k) + k^2 \operatorname{sn}^2(u \mid k) = 1\]

Using these identities, we can express \(\operatorname{cn}\) and \(\operatorname{dn}\) in terms of \(S\):

\[\operatorname{cn}(f + \omega \mid k_{01}) = \sqrt{1 - \operatorname{sn}^2(f + \omega \mid k_{01})} = \sqrt{1 - S^2}\] \[\operatorname{dn}(f + \omega \mid k_{01}) = \sqrt{1 - k_{01}^2 \operatorname{sn}^2(f + \omega \mid k_{01})} = \sqrt{1 - k_{01}^2 S^2}\]

By substitution,

\[S'^2 = \left( \sqrt{1 - S^2} \cdot \sqrt{1 - k_{01}^2 S^2} \right)^2\]

And therefore,

\[S'^2 = (1 - S^2)(1 - k_{01}^2 S^2)\]

Thoughts

Today is definitely tiring… It’s Friday already and I have 7 weeks to go! I will probably take a break tomorrow and on Sunday.

This week is rather promising, and I have made more progress than I expected myself to! (Especially the coding part). I will start my write up probably soon. Putting content here definitely helps!

Credits

The whole post is based on the book Integrable Systems in Celestial Mechanics. I only highlight the important parts. Part of the content related to jacobi elliptic functions is from wikipedia.

I would also like to thank Dr Jenni Smillie for her guidance and support duing this project.