Conservations in Physics - Noether’s Theorem

This article is built for two types of audiences. The first part is quite involved and assumes knowledge of advanced classical mechanics (for example Lagrangian Dynamics and Variational Principle). The second part is more mild and is targeted for students with some experiences in basic calculus skills.

Proof of Noether’s Theorem in translational symmetry

The proof of Noether’s Theorem is quite involved. However, it is a good exercise to show the proof for one-dimensional case.

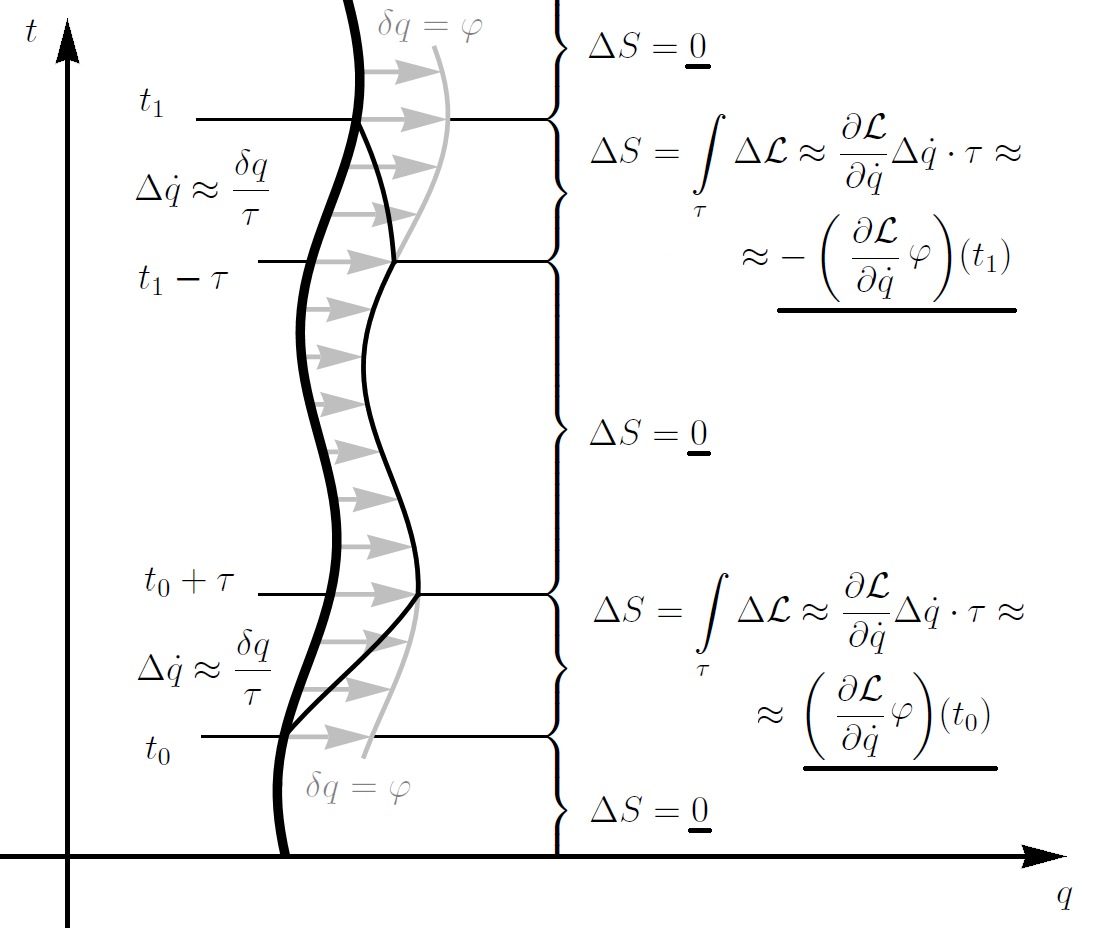
Assume the system has translational symmetry: \(\phi: q \mapsto q + \delta q\). Now assume a trajectory travels from the more bolded line (in the image below) to the less bolded line, in time \(\tau\).

Using the definition of action: \(S = \int L\), we arrive at \(\Delta S=\int \Delta L\). If \(L\) only depends on \(\dot{q}\), \(\Delta L \approx \left(\frac{\partial L}{\partial \dot{q}}\right) \Delta \dot{q}\). From the image, it is also obvious that \(\Delta \dot{q}=\pm \frac{\delta q}{\tau}\).

\[\Delta S=\int \Delta L \approx \int \frac{\partial L}{\partial \dot{q}} \Delta \dot{q} \approx \int \frac{\partial L}{\partial \dot{q}}\left( \pm \frac{\delta q}{\tau}\right) \approx \pm \frac{\partial L}{\partial \dot{q}} \delta q= \pm \frac{\partial L}{\partial \dot{q}} \varphi .\]

As \(\Delta S\) is \(0\), we have:

\[\left(\frac{\partial L}{\partial \dot{q}} \varphi\right)\left(t_0\right)=\left(\frac{\partial L}{\partial \dot{q}} \varphi\right)\left(t_1\right)\]

This result is also verified in my other post.

(Image from Wikipedia)

Exercises for the readers

• Explain the reason for the \(\pm\) sign in \(\Delta L\). What does it correspond to? (Difficulty: University Year 1)
• Why is the total action equal to \(0\)? (Difficulty: University Year 2-3)
• Why is \(\dot{q}\) assumed to be the only contributing term? (Hint: \(\tau\) is taken to appraoch \(0\)) (Difficulty: University Year 2-3)

Finding the constant in rotational symmetry

\[\hat{r}=\cos (\theta) \hat{x}+\sin (\theta) \hat{y}, \quad \hat{\theta}=-\sin (\theta) \hat{x}+\cos (\theta) \hat{y} .\]

By Chain Rule,

\[\dot{\hat{r}}=\dot{\theta}[-\sin (\theta) \hat{x}+\cos (\theta) \hat{y}]=\dot{\theta} \hat{\theta}, \quad \dot{\hat{\theta}}=\dot{\theta}[-\cos (\theta) \hat{x}-\sin (\theta) \hat{y}]=-\dot{\theta} \hat{r} .\]

And

\[\underline{\dot{r}}=\frac{d}{d t}(r \hat{r})=\dot{r} \hat{r}+r \dot{\hat{r}}=\dot{r} \hat{r}+r \dot{\theta} \hat{\theta}\]

Further Differentiation yields:

\[\begin{aligned} \underline{\ddot{r}}=\frac{d}{d t}(\dot{r} \hat{r}+r \dot{\theta} \hat{\theta}) & =\ddot{r} \hat{r}+\dot{r} \dot{\hat{r}}+\dot{r} \dot{\theta} \hat{\theta}+r \ddot{\theta} \hat{\theta}+r \dot{\theta} \dot{\hat{\theta}} \\ & =\ddot{r} \hat{r}+\dot{r} \dot{\theta} \hat{\theta}+\dot{r} \dot{\theta} \hat{\theta}+r \ddot{\theta} \hat{\theta}-r \dot{\theta} \dot{\theta} \hat{r} \\ & =\left(\ddot{r}-r \dot{\theta}^2\right) \hat{r}+(2 \dot{r} \dot{\theta}+r \ddot{\theta}) \hat{\theta} \end{aligned}\]

Since the force is a central force, we have:

\[m\left(\ddot{r}-r \dot{\theta}^2\right) \hat{r}+m(2 \dot{r} \dot{\theta}+r \ddot{\theta}) \hat{\theta}=F_r(r) \hat{r} .\]

We can quickly identify two equations:

\[\begin{aligned} \ddot{r}-r \dot{\theta}^2 & =F_r(r) / m \\ 2 \dot{r} \dot{\theta}+r \ddot{\theta} & =0 . \end{aligned}\]

From the second equation:

\[\frac{1}{r} \frac{d}{d t}\left(r^2 \dot{\theta}\right)=0 \quad \Longrightarrow \quad r^2 \dot{\theta} \equiv h=\text { const }\] \[\underline{L}=\underline{r} \times \underline{p}=m r \hat{r} \times \underline{\dot{r}}=m r \hat{r} \times(\dot{r} \hat{r}+r \dot{\theta} \hat{\theta})=m r \hat{r} \times r \dot{\theta} \hat{\theta}=m r^2 \dot{\theta} \hat{n} \equiv m h \hat{n}\]

Hence:

\[r^2 \dot{\theta} \equiv h=\frac{|\underline{L}|}{m}\]

Exercises for the reader

• What is being conserved in rotational symmetry? (Difficulty: HKDSE F4)
• Show the results above using Lagrangian Dynamics. (This is a much faster method) (Difficulty: University Year 2-3)

Credits

This section is heavily inspired by 3 sources - Prof Arjun Berera’s Introductory Dynamics course, Dr Jenni Smillie’s Lagrangian Dynamics, and the wikipedia page on Noether’s Theorem.

Last Updated - 3/6/2024