A Proof of the Existence of the Figure-8 Orbit using Actions and the Shape Sphere

This is the nineth post on my summer research about three-body problems. Today we are discussing the existence of the Figure-8 orbits. This will involve the discuss of Shape-Spheres (I mentioned in a previous post), as well as minimizers and actions.

This is my previous post about the Sundman Series if you have missed it.

Overview of the Proof of Figure-8 Orbits

To begin the discussion, I will outline the proof of the existence of a figure-8 orbit:

• In the shape-sphere space, find minimizers travelling from Euler Central Configuration to isosceles configuration. This corresponds to \(1/12\)th of the full orbit.
• Let \(A_c\) be the minimum action of a path with any collisions. Show that \(A< A_c\) for all actions of paths without collisions.
• Use \(12\) “copies” of the “\(1/12\)“th path mentioned above to form a whole orbit in the shape-sphere space. Argue that it is continuous.
• Translate the path in shape sphere to a path in the euclidean space. Argue that it corresponds to a figure-8 orbit.

This orbit is extremely special because it appears to be one of the very few choreographies to be stable. The other significant example is shown in the previous post (Lagrange).

Finding Minimizers

Definitions

We define an action in the shape sphere as:

\[A = \int_{0}^{T} (\frac{1}{2}K+U) \ dt\]

over the subspace of \(\Lambda\) of \(H^1([0,T], \chi)\), where \(H^1\) refers to a Sobalev Space. A important fact is about the Sobalev Space is that the function itself and its time derivative are both Square Integrable, and \(\chi\) refers to:

\[\chi = \{ x=(x_1, x_2, x_3) \in (\mathbb{(C)}^3), \sum_{i=1}^{3} x_i =0 \}.\]

We are starting at an Euler configuration and end at an isosceles configuration with arbitary size.

One twelfth of the orbit is obtained by minimizing this action.

Below we will present the skeleton of the proof:

Proving the orbit from \(T=0\) to \(T=\frac{\bar{T}}{12}\) has no collisions

Step 1

If a path in \(\Gamma\) which minimizes such an action has collisions (either double or triple), its action would exceed \(A_2\), where \(A_2\) is the action of the two-body collinear solution in which two unit masses start at collision and end with zero velocity at a time \(T\) later, the center of mass being fixed throughout.

Step 2

The Euler Equipotential Length satisfies \(l_0< \frac{\pi}{5}\).

Step 3

If Step 2 holds, the minimum \(A\) of the actions of equipotential test paths is smaller than \(A2\).

From the highlighted parts above the reader can clearly see such a path has no collisions.

In other words, \(a< A_2 < A_{\text{Collision}}\) and in fact, \(A_2\) is the infimum of all paths in \(H^1([0,T], \chi)\) with collisions.

Proving a complete orbit can be obtained by “copy-pasting” the orbit above for \(12\) times

The main difficulty is to prove the end-points of each orbits are well behaved.

The first task is to prove that the minimizing arc is orthogonal to the two man ifolds E3 and M1 constraining its endpoints.

Recall that:

\[\delta A = \epsilon \left[ \frac{\partial L}{\partial \dot{x}} \eta \right]_0^T + \epsilon \int_0^T \left(\frac{\partial L}{\partial x} - \frac{d}{dt} \frac{\partial L}{\partial \dot{x}}\right) \eta \ dt\]

Normally we treat \(\left[ \frac{\partial L}{\partial \dot{x}} \eta \right]_0^T\) as \(0\) immediately through the assumption \(\eta(0)=0\) and \(\eta(T)=0\), but this cannot be done here as E3 and M1 are not points. Rather, they form a line in the shape sphere.

We must have:

\([\frac{\partial L}{\partial \dot{x}} \vert _{T=0}] (\eta) = 0\).

As \(\frac{\partial L}{\partial \dot{x}}\) moves along the minimizing curve and \(\eta\) is on the tangent plane of the manifolds, we can conclude that the minimizing arc is orthogonal to the two manifolds E3 and M1 constraining its endpoints.

Converting the orbit on shape sphere to an actual orbit (and show it is the Figure-8 Orbit)

Showing the orbit is periodic

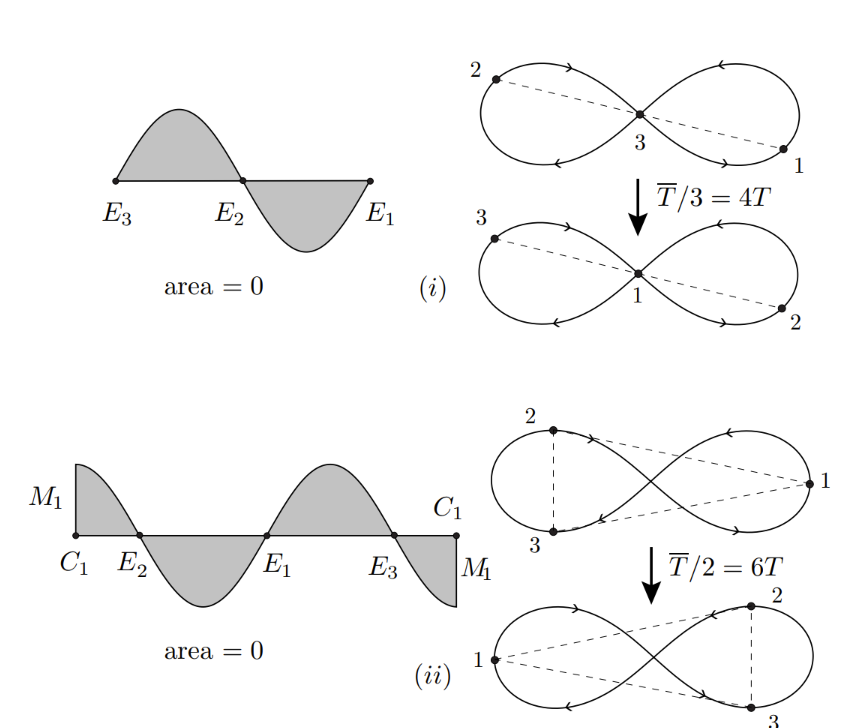
We know that our shape sphere is closed. Then the initial and final triangles in the plane are similar (as they correspond to the same point on the shape sphere). How to find the angle of rotation which relates these two triangles?

The area rule states that the angle of rotation (as stated above) is equal to twice the spherical area enclosed by the shape curve.

The graph below shows what happens when we start and end on the equator (corresponding to \(E_i\), where \(i\) can be \(1, 2, 3\)) or starting and ending on the Meridian Line \(M_1\). For a clearer illustration, the points \(E_i\) and the meridian line \(M_1\) are defined below:

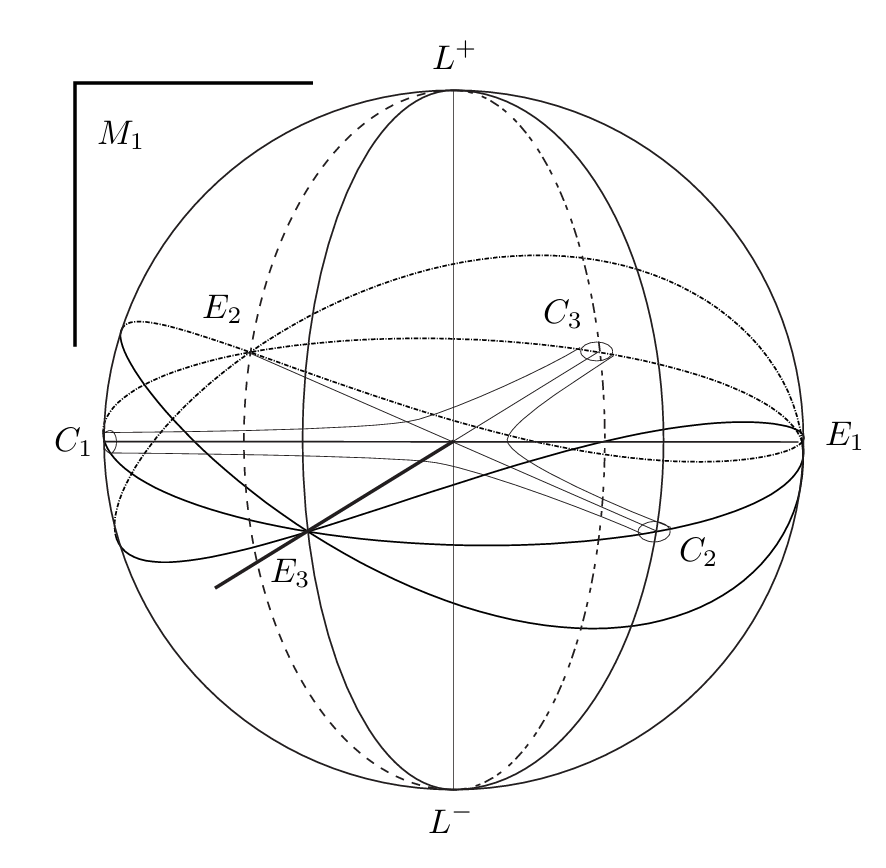
From the graph below, it is clear that the three particles differ only by a relative phase.

Showing there aren’t “unpleasant” features in the orbit

It can be shown that the angular momentum for each particle remains strictly negative for \(0< t < \bar{T}/2\). As the angular momentum is proportional to \(r^2 \dot{\omega}\), \(\dot{\omega}\) is negative, and hence \(\omega\) decreases. It can be seen that loops cannot occur.

Therefore, the Figure-8 shape is the only possible orbit.

Progress

Doing such a long project is definitely quite tiring and I am slightly burnt out. It is very nice, however, that I am progressing much faster than I originally planned.

Credits

This proof is not original and is based on the paper “A remarkable periodic solution of the three-body problem in the case of equal masses” and the presentation “I’ve Got a Three-Body Problem”

I would like to thank Dr Jenni Smillie for her guidance and support duing this project.