Sundman’s Power Series Solution to the Three Body Problem (Part I)

This is the seventh post on my summer research about three-body problems. Today we are discussing Karl F. Sundman’s Solution to the Three Body Problem. It almost provides a general solution to the Three Body Problem, but its slow convergence renders it completely useless.

This is my previous post about the problem of two fixed centers if you have missed it.

Summary of Important Points in Sundman’s Paper

• In a double collision, the distance to the non-participating third body remains bounded.
• In order for a triple collision to occur, the area integral of the system must equal zero.
• The velocity and acceleration of the colliding body tends toward infinity at the point of double collision.
• The unit vector along the radius joining the two colliding bodies tends to a limit.
• Singularities in the equations of motion can be removed at one of the bodies by the introduction of the independent variable “\(u\)”.
• An independent variable “\(w\)” was found such that all the singularities of the motion were removed, allowing any number or combinations of double collisions to occur. (This is needed below!)
• Power series solutions for the coordinates of the three bodies can be developed in powers of \(w-\bar{w}\).
• The power series solutions were found to converge, although extremely slowly.

Construction and Convergence of \(w\)

How singularities arise

As seen above we can define an independent variable “\(w\)” that can remove singularities. But why are there singularities while using “\(u\)”?

This is because of the assumption that \(m_0\) and \(m_1\) are the colliding bodies. In the equation of motions, terms such as \(\frac{1}{r_0}\) and \(\frac{1}{r_1}\) appear (proof omitted), which causes singularities when \(r_0=0\) or \(r_1=0\).

Definition of \(w\)

We define:

\[dt= \Gamma dw\]

with the initial conditions \(w=0\) when \(t=0\).

Where \(\Gamma\) can be defined as:

\[\Gamma = (1-e^{\frac{-r_0}{l}})(1-e^{\frac{-r_1}{l}})(1-e^{\frac{-r_2}{l}})\]

The symmetry of this set-up causes \(r_0\) to be indistinguishable from \(r_1\) and \(r_2\). The next step is to explore its convergence.

Convergence as a strip

After some complicated analysis which I won’t show here (the interested reader can read the extremely lengthy proof here), we arrive at \(\vert w - \bar{w} \vert < \Omega\), where \(\Omega\) is real and \(\bar{w}\) is the value of \(w\) when \(t \to \bar{t}\). This corresponds to a convergence strip of \(2 \Omega\).

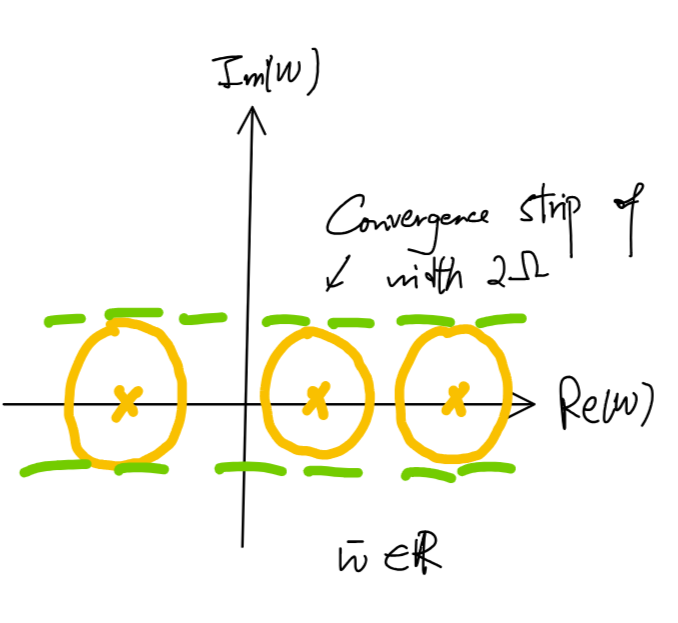
Mapping the strip to a disc through Möbius Transformation

In power series, it is a convention to express the “convergence area” as a disc. How do we map a strip to a disc? This can be done using Möbius Transformation in Complex Analysis.

We can denote the strip as: \(S = [s : \text{Im}(s) \leq \beta]\).

Notice that \(g(z) = e^{\frac{(\frac{\pi}{2})s}{\beta}}\) maps \(S\) to the right half plane.

Next, notice that for the right half plane, \(\vert z-1 \vert < \vert z+1 \vert\). This implies \(h(z)=\frac{\vert z-1 \vert}{\vert z+1 \vert}<1\) maps the right half plane to the unit disc. \(h(g(z))\) thus maps \(S\) to the unit disc.

Note that:

\[w = \frac{2 \Omega}{\pi} \log{\frac{1+ \tau}{1- \tau}}\]

is the expression of \(w\) in terms of \(\tau\). This is less useful however as \(\tau\) is the unknown. It is a good exercise to show, however, that when \(\vert \tau \vert < 1\), \(- \infty < w < \infty\).

This transformation results in many points being mapped near the boundary of the region of convergence. This causes the slow convergence.

This power series only work if \(c \neq 0\), where \(c\) is equal to:

\[m_0 (\vec{r_0} \times \vec{v_0}) + m_1 (\vec{r_1}\times \vec{v_1}) + m_2 ( \vec{r_2} \times \vec{v_2}) = \vec{c}\]

The astute reader can notice this is indeed the sum of angular momentum.

Sundman’s Solution for the Three Body Problem practically works for essentially all cases (even collisions between two bodies, but not collision between three bodies, as that will result in \(c=0\)).

The problem is the convergence of the series is too slow (the number of terms can reach \(10^{8 \times 10^6}\) for just a single decimal of accuracy!) (See Belorizky’s Analysis).

Summary

An independent variable \(w\) that is well-defined for any double collisions has been found. It converges in a strip with width \(2 \Omega\), which is then Möbius-transformed to a unit disc with a new variable \(\tau\). This is a general solution for the three body problem, as long as the sum of angular momentum is not equal to \(0\). However its slow convergence causes a problem.

Progress

Reading literature takes me a lot of time and it’s quite tiring. Again, it is good that I keep a blog running so I can always document my thoughts before I forget. I have been working on the BHH orbits also, which I have included below with the corresponding shape sphere (in 2 angles):

Credits

This post is based on the papers by Donald K.Yeomans and Peter Senchyna.

I would like to, again, thank Dr Jenni Smillie for her guidance and support duing this project.