Thermodynamic Potentials and Maxwell Relations
Below we will derive the 4 theromodynamic potentials, as well as provide a short derivation of the Maxwell Relations.
Throughout this section we have assumed the system is closed (no exchange in matter). We need to consider the chemical potential energy if the system is open.
Central Equation of Thermodynamics
Consider First Law of Thermodynamics, \(dU=dQ-dW\). Now express \(dW=PdV\). Now recall that in a reversible process,
\[\begin{align*} dS&=\frac{dQ}{T}\\ \implies TdS&=dQ \end{align*}\]Recombing will lead us to:
\[dU=TdS-PdV\]Enthalpy
We typically consider enthalpy to be the energy function that minimises in an isentropic \((dS=0)\) and isobaric process \((dP=0)\). We can express \(dH\) (differential in enthalpy) in terms of \(dU\). How to get rid of the extra \(dV\) in \(dU\)?
Consider:
\[H=U+PV\]Then,
\[\begin{align*} dH&=dU+d(PV) \\ &=TdS-PdV+PdV+VdP \\ &=TdS+VdP \end{align*}\]Gibbs Free Energy
Gibbs Free Energy is minimised in an isothermal \((dT=0)\) and isobaric \((dP=0)\) process. This can be represented as:
\[G=U+PV-TS=H-TS\]The reader can verify that this leads to: \(dG=VdP-SdT\).
Helmholtz Free Energy
Helmholtz Free Energy is minimised in an isothermal \((dT=0)\) and isochoric process \((dV=0)\) . This is left as an exercise for the readers.
Trick to Memorize
I used to struggle to memorize these relationships before I stumple upon this image:
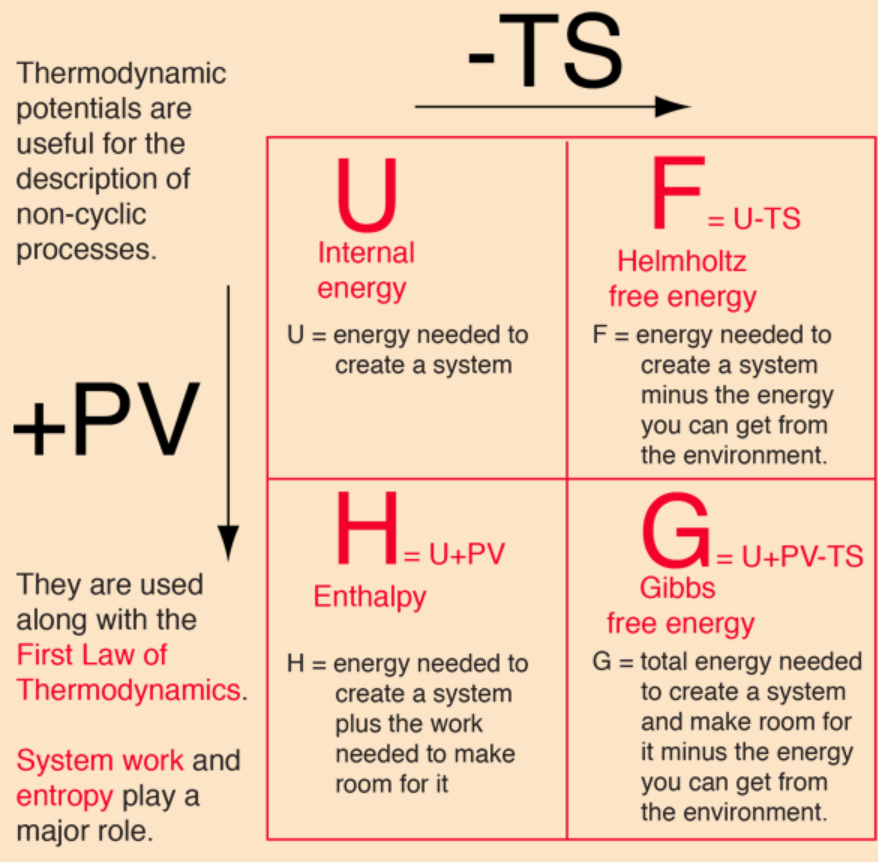
Credits to Hyperphysics.
An Example of Maxwell Relation
Recall:
\[df = \sum_{i} \frac{\partial f}{\partial x^i} dx^i.\]From \(dG = -S dT + V dP\), we can easily see:
\[\left( \frac{\partial G}{\partial T} \right)_P = -S, \quad \left( \frac{\partial G}{\partial P} \right)_T = V\]Taking the mixed partial derivatives:
\[\frac{\partial}{\partial P}\left(\frac{\partial G}{\partial T}\right)_P = \frac{\partial}{\partial P} (-S) = -\left(\frac{\partial S}{\partial P}\right)_T\] \[\frac{\partial}{\partial T}\left(\frac{\partial G}{\partial P}\right)_T = \frac{\partial}{\partial T} (V) = \left(\frac{\partial V}{\partial T}\right)_P\]By Symmetry of Second Derivatives, we have:
\[-\left(\frac{\partial S}{\partial P}\right)_T = \left(\frac{\partial V}{\partial T}\right)_P\]So, the Maxwell relation derived from \(G\) is:
\[\left(\frac{\partial S}{\partial P}\right)_T = -\left(\frac{\partial V}{\partial T}\right)_P\]This is highly useful as \(dS\) is not easily measurable but \(dV\) is. There are 3 more sets of Maxwell Relations, each corresponding to a thermodynamic potential. This is left as an exercise for the reader.
