Problem of Two Fixed Centers (Part II)

This is the sixth post on my summer research about three-body problems. Today we are continuing our discussion on the problem of Two Fixed Centers. I have a brief introduction on this particular problem here.

This is my previous post about shape spheres if you have missed it.

Converting from Cartesian Coordinates to Prolate Spheroidal Coordinates System

As mentioned before, rewriting in spheroidal coordinates, we have:

\[r \sin \theta=x= \pm \sqrt{R^2-b^2} \sin \sigma\]

\(r \cos \theta=z=R \cos \sigma\).

Notice that the case for \(x < 0\) is taken care of by the \(\pm\) sign, so we only need to consider the cases for \(x > 0\).

Using \(R = \frac{z}{\cos {\sigma}}\), we can substitute one of the equations into the other:

\[\begin{aligned} x &= \sin \sigma \sqrt{\left(\frac{z}{\cos \sigma} \right)^2 - 1} \\ &= \sqrt{\frac{z^2 - \cos^2 \sigma}{\cos^2 \sigma}} \sin \sigma \\ x^2 &= \frac{(z^2 - 1 + \sin^2 \sigma)(\sin^2 \sigma)}{1 - \sin^2 \sigma} \\ x^2 &= \sin^2 \sigma (x^2 + z^2 - 1 + \sin^2 \sigma) \end{aligned}\]

Where we have used \(\cos{\sigma} = \sqrt{1- \sin^2{\sigma}}\) (So it is not valid in some regions!). By letting \(u=\sin^2{\sigma}\), we have:

\[u^2+(x^2+z^2-1)u-x^2=0\]

Where we can continue to solve using the Quadratic Formula. We arrive at:

\[\arcsin{\sqrt{u}} = \sigma_1\]

Where \(u = \frac{-(x^2 + z^2 - 1) + \sqrt{(x^2 + z^2 - 1)^2 + 4x^2}}{2}\).

Note that this will only return \(\sigma\) outside of \(\frac{\pi}{2}< \sigma < \frac{3 \pi}{2}\), ie for \(z>0\), which means that \(z\) is always positive, as \(z= R \cos{\sigma}\), and \(\cos{\sigma}\) is only negative in the range \(\frac{\pi}{2}< \sigma < \frac{3 \pi}{2}\).

Let \(\sigma\) be the angle required.

The other scenario (\(z<0,\)\frac{\pi}{2}< \sigma < \frac{3 \pi}{2}\() can be solved by letting\)\sigma = \pi-\sigma_1\(for\)z<0\(, and\)\sigma = \sigma_1\(for\)z>0$$.

\(R\) can be easily found given \(\sigma\).

Results

Given this trajectory:

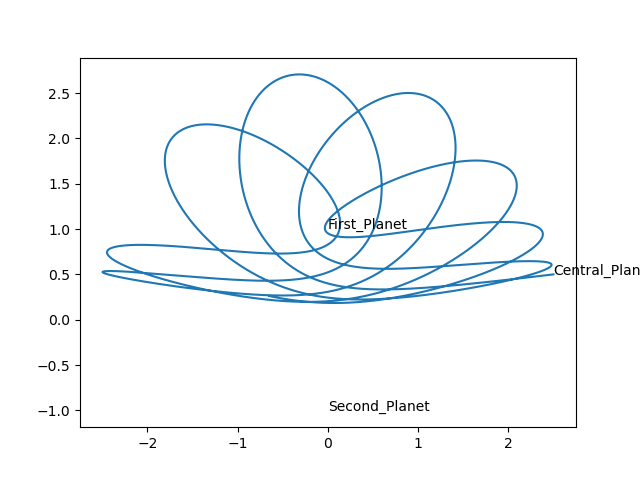
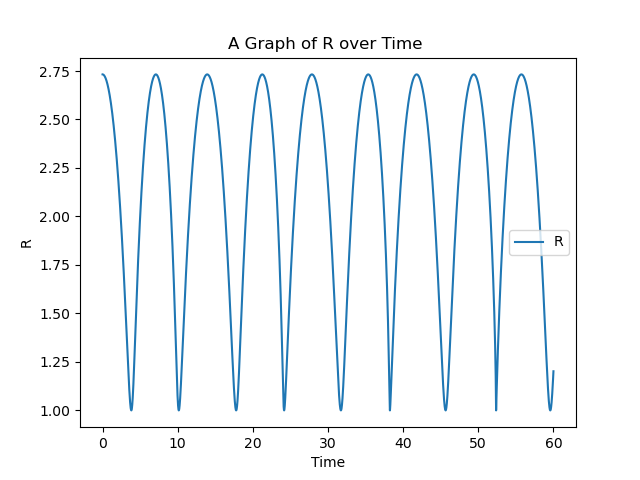
We can plot the \(R\) graph over time:

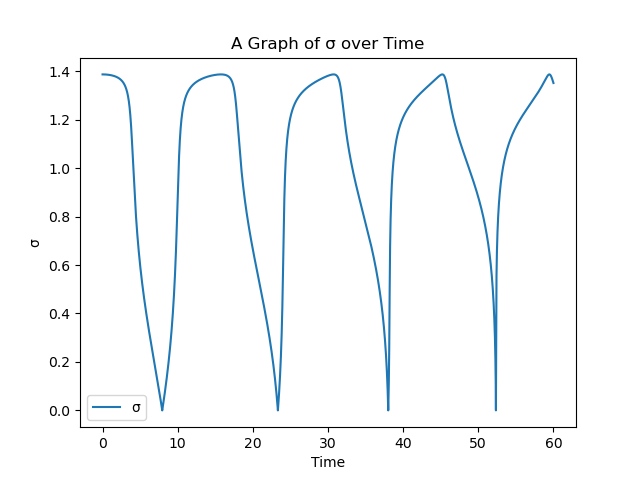
\(\sigma\) graph over time:

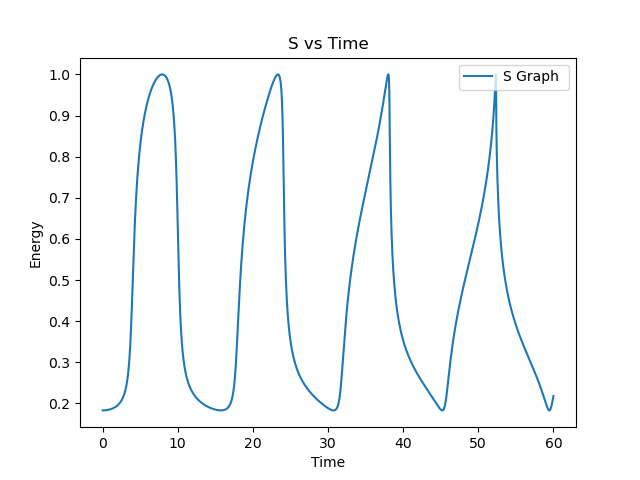
And \(S\) graph over time (\(S= \cos{\sigma}\)):

Issues

It seems like the central particle never passes the lagrange points, so it is only attracted by one of the two fixed masses. This disagrees with the theory, as \(S\) should be proportional to \(\operatorname{sn}\), which implies \(\sigma\) should go through all \(4\) quadrants, whereas it only goes pass \(2\) now. This may be due to a wrong assumption - The way I implemented the problem of two fixed masses is I kept two of the particles fixed, but in reality I should achieve this by setting two of the masses extremely high. The other assumption that may be wrong is initial velocity being \(0\). I believe a high velocity can enable the particle to pass through the lagrange points!

Progress

I am stuck on this part for quite a while as it is quite hard to map the constants in the book to my code. I also spent quite a while on shape spheres and I will spend more time on the theory. In the next few weeks, I will spend time understanding the Sundman Series. I expect it to be extremely computationally challenging.

Credits

Again, the whole post is based on the book Integrable Systems in Celestial Mechanics.

I would like to, again, thank Dr Jenni Smillie for her guidance and support duing this project.