Problem of Two Fixed Centers (Part III)

This is the eleventh post on my summer research about three-body problems. Today we are continuing our discussion on the problem of Two Fixed Centers. Please note that this is the third part of the series. The first part is here and the second part is here.

New Types of Orbits

Previously we mentioned:

””” It seems like the central particle never passes the Lagrange points, so it is only attracted by one of the two fixed masses. This disagrees with the theory, as \(S\) should be proportional to \(\operatorname{sn}\), which implies \(\sigma\) should go through all \(4\) quadrants, whereas it only goes past \(2\) now. This may be due to a wrong assumption - The way I implemented the problem of two fixed masses is I kept two of the particles fixed, but in reality, I should have achieved this by setting two of the masses extremely high. The other assumption that may be wrong is the initial velocity being \(0\). I believe a high velocity can enable the particle to pass through the Lagrange points! “””

Indeed the assumption that initial velocity is \(0\) is inaccurate. Meticulously changing the initial velocity will lead to two new types of orbits - Lemniscate and Planetary.

But first I will introduce two constants of motion: \(G\) and \(H\):

\[\begin{aligned} \quad G&=\frac{1}{2}\left(x p_y-y p_x\right)^2+\frac{1}{2} d^2 p_x^2+d x\left(\frac{m_1}{\sqrt{(x+d)^2+y^2}}-\frac{m_2}{\sqrt{(x-d)^2+y^2}}\right) \\ H&=\frac{1}{2}\left(p_x^2+p_y^2\right)-\frac{m_1}{\sqrt{(x+d)^2+y^2}}-\frac{m_2}{\sqrt{(x-d)^2+y^2}} . \end{aligned}\]

The reader can realize \(H\) is simply the Hamiltonian (measures energy), whereas \(G\) is a constant of motion discovered by Euler.

In the paper Syzygies In The Two Center Problem, it has been shown that the value of \(H\) and \(G\) dictates the type of orbit. \(S\) refers to Satellite and it is indeed what we discovered a few weeks ago. \(L\) refers to Lemniscate and \(P\) refers to Planetery. All of these are shown below:

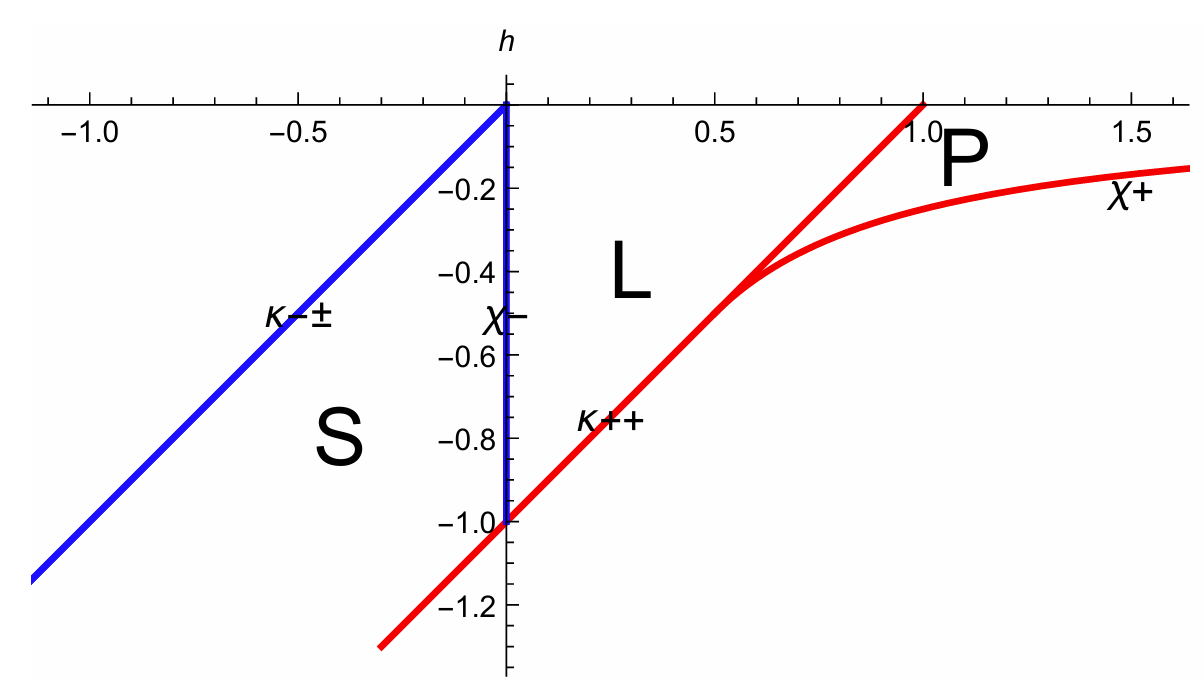
Figure from Syzygies In The Two Center Problem.

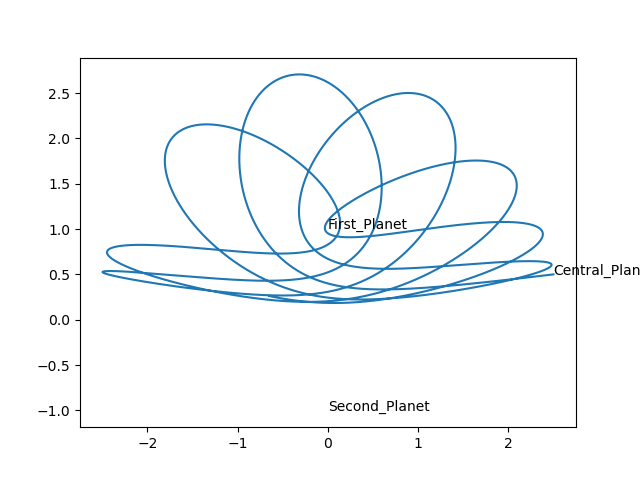
Satellite

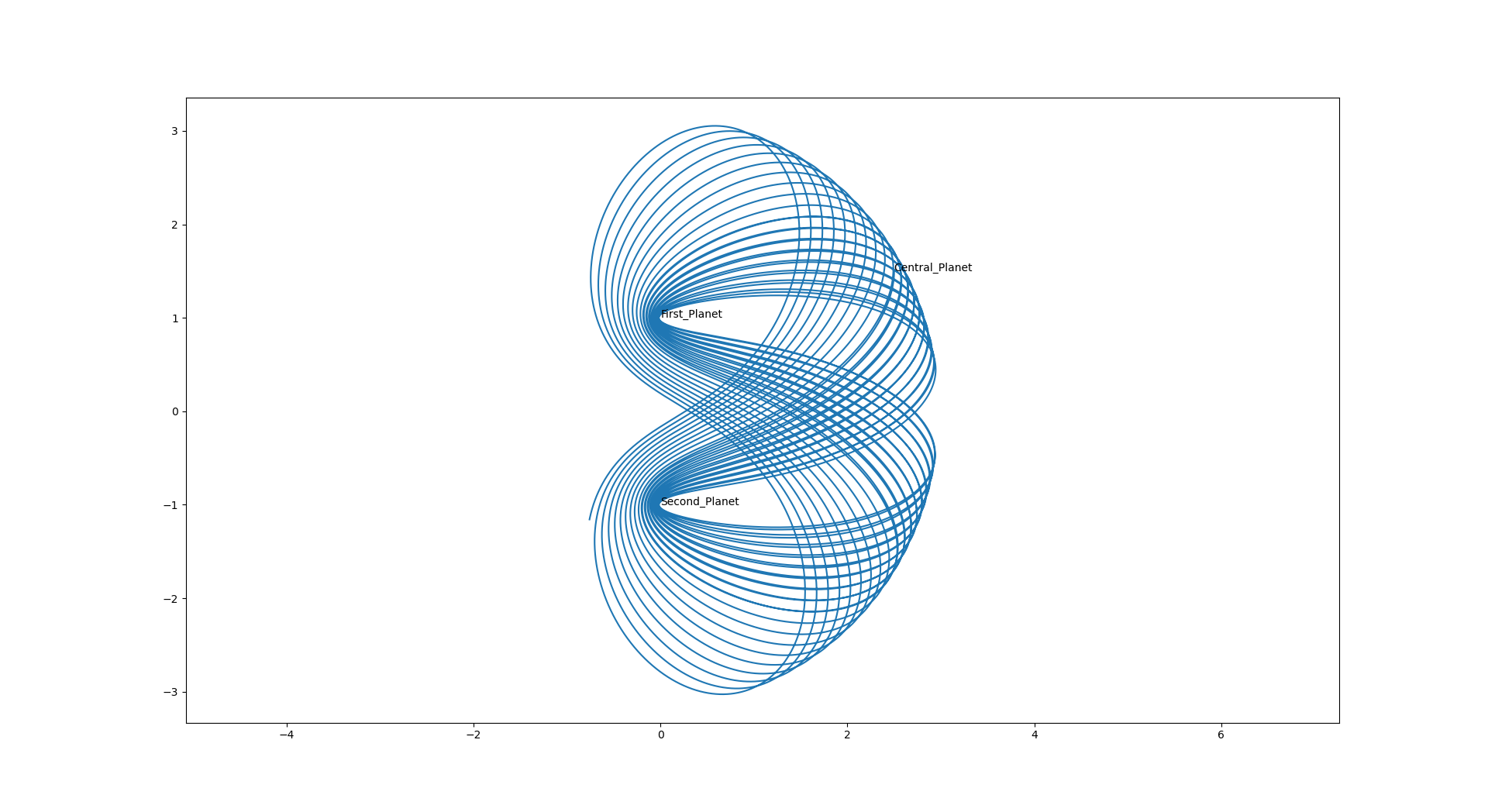
Lemniscate

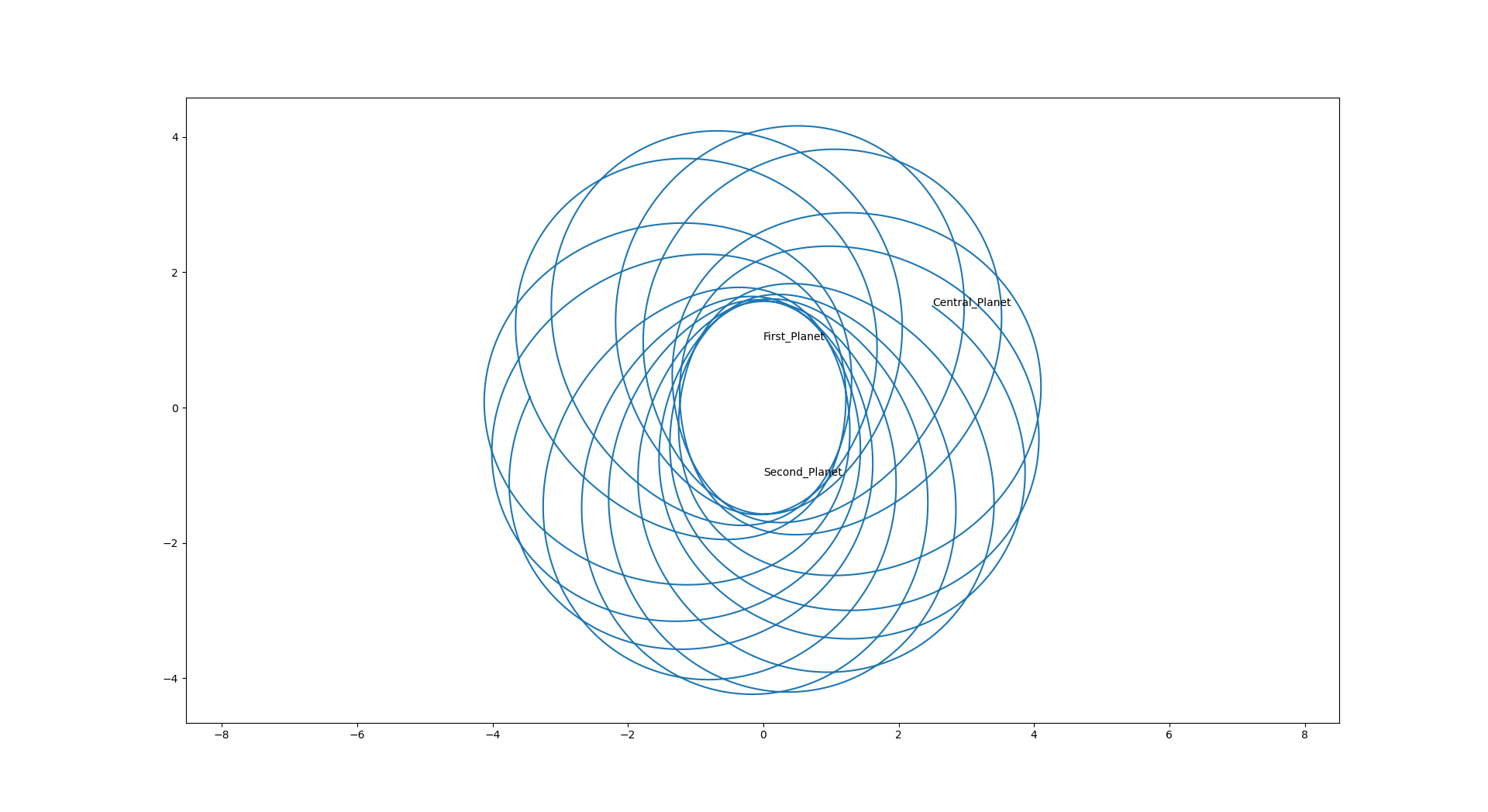
Planetary

To be continued…

So now \(S\) appears to have the correct range. However, \(S\) still looks rather irregular and doesn’t quite correspond to \(\operatorname{Sn}\).

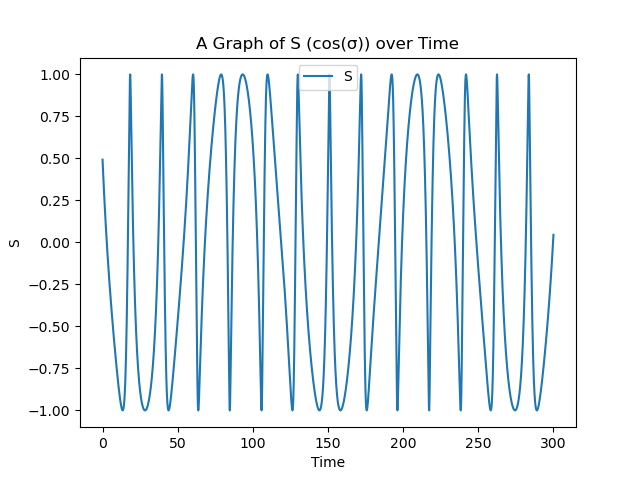
The S-Graph for Planetary Orbits

As for the values for \(e\) (Please refer to the book Integrable Systems in Celestial Mechanics, \(e>1\) and \(e<1\) refer to different types of orbits), it seems like Lemniscate orbit has a significantly higher \(e\) (around \(e = 2.5\)), while satellite orbit corresponds to the lowest \(e\), around \(e = 0.98\). Planetary orbit corresponds to \(e = 1.08\). The significance of this will be explored next week.

Future Work

 - Initial conditions that correspond to each of \(S\), \(L\) and \(P\) should be plotted. I hope this will lead to the discovery of new types of orbits. Extend this to the case where the two fixed centers have different masses.  - Figure out if the mass of the test particle matters.

Progress

Another tiring week.

I am very happy that I am making progress much faster than I originally expected. It may be time to start thinking about my final report. As this project will end in \(3\) weeks, I have around 1.5 months to write the final report and the poster, so there is plenty of time. Writing a skeleton early is a good idea, however. This is the motivation for me to update the website often.

I only have \(3\) more weeks to make some original contribution to this problem, but this seems very unlikely at this point, which is very disappointing. I’ll see what I can do.

Credits

I am inspired by the paper Syzygies In The Two Center Problem and the book Integrable Systems in Celestial Mechanics.

I would like to thank Dr. Jenni Smillie for her guidance and support during this project.